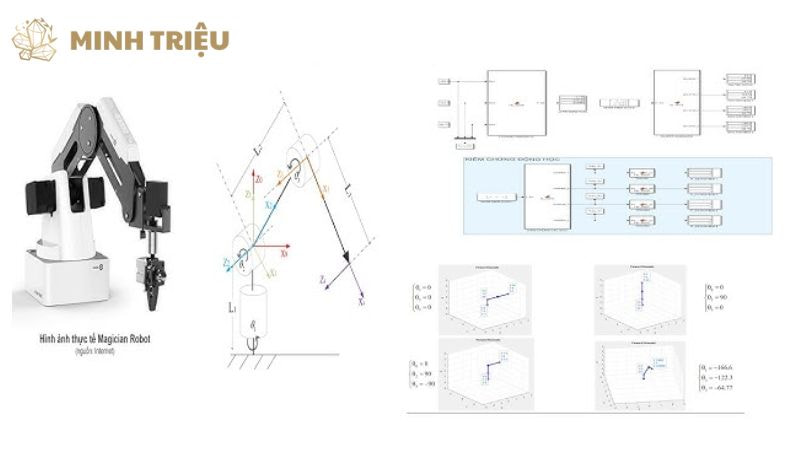
Robot công nghiệp
Nguyên lý động học robot (kinematics): Chìa khóa điều khiển và ứng dụng hiệu quả
Động học robot là nền tảng quan trọng trong robot học, tập trung nghiên cứu chuyển động mà không xét đến lực tác động. Nó cung cấp cơ sở toán học để xác định vị trí và hướng của các khâu robot, đóng vai trò then chốt từ thiết kế, mô phỏng đến vận hành. Bài viết này trình bày các khái niệm chính như động học thuận, động học nghịch, phương pháp giải bài toán động học và ứng dụng trong công nghiệp. Bài viết cũng đề cập đến tối ưu hóa, thách thức hiện tại và tiềm năng phát triển của động học robot trong bối cảnh công nghiệp 4.0.
1. Động học thuận (Forward Kinematics)
Động học thuận xác định vị trí và hướng của khâu công tác cuối (end-effector) của robot dựa trên các giá trị đã biết của khớp (góc quay hoặc quãng trượt). Đây là một bài toán cơ bản, trong đó, ta có thông tin về cấu hình của robot (chiều dài các khâu, góc giữa các khớp) và các giá trị của các khớp động (ví dụ: góc quay của khớp quay, quãng trượt của khớp trượt) và mục tiêu là tính toán chính xác vị trí, hướng (tư thế) của dụng cụ hoặc thiết bị gắn ở cuối cánh tay robot.
Ví dụ điển hình là một robot 2 bậc tự do, nơi chúng ta có thể dễ dàng tính toán vị trí đầu cuối nếu biết chiều dài hai khâu và hai góc quay tại các khớp.
1.1. Phương pháp biểu diễn
Phương pháp biểu diễn chính được sử dụng trong động học thuận là Ma trận biến đổi thuần nhất (Homogeneous Transformation Matrix) và tham số Denavit-Hartenberg (DH Parameters). Việc sử dụng các công cụ toán học này cho phép mô tả một cách hiệu quả mối quan hệ không gian giữa các khâu của robot.
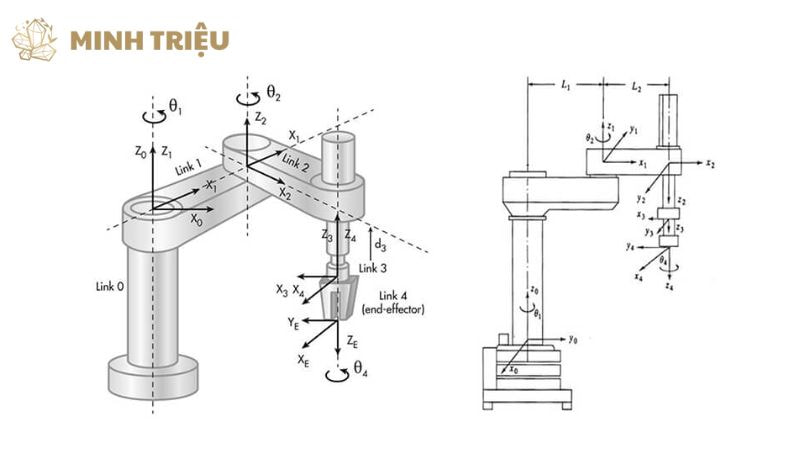
Ma trận biến đổi thuần nhất
Ma trận biến đổi thuần nhất là một công cụ toán học mạnh mẽ cho phép biểu diễn đồng thời cả vị trí và hướng của một hệ tọa độ so với một hệ tọa độ khác trong không gian ba chiều. Ma trận này là một ma trận 4×4 bao gồm một ma trận quay R (kích thước 3×3) và một vector t (kích thước 3×1) biểu diễn vị trí tịnh tiến. Cụ thể, R mô tả sự định hướng của hệ tọa độ hiện tại so với hệ tọa độ gốc, trong khi t biểu thị vị trí của gốc hệ tọa độ hiện tại so với hệ tọa độ gốc.
Để xác định tư thế của khâu công tác cuối, ta thực hiện nhân liên tiếp các ma trận biến đổi thuần nhất từ gốc robot cho đến khớp cuối cùng, trong đó mỗi ma trận đại diện cho biến đổi giữa hai khâu kề nhau. Ví dụ, để xác định vị trí của một điểm trong không gian của khâu thứ n, chúng ta nhân ma trận biến đổi từ khâu gốc đến khâu 1, rồi từ khâu 1 đến khâu 2, và cứ thế tiếp tục cho đến khâu n.
Tham số Denavit-Hartenberg (DH Parameters)
Tham số Denavit-Hartenberg là một công ước chuẩn hóa toàn cầu để thiết lập hệ tọa độ cho từng khớp của robot, từ đó đơn giản hóa quá trình thiết lập các ma trận biến đổi thuần nhất. Phương pháp này xác định bốn tham số hình học đặc trưng cho mỗi khâu của robot:
- a: Chiều dài khâu (khoảng cách vuông góc giữa trục Zi−1 và Zi).
- α: Góc xoắn khâu (góc từ trục Zi−1 đến Zi quanh trục Xi−1).
- d: Quãng trượt khớp (khoảng cách từ gốc của hệ tọa độ i−1 đến giao điểm của trục Xi−1 với trục Zi).
- θ: Góc khớp (góc từ trục Xi−1 đến Xi quanh trục Zi). Sự tiện lợi của việc sử dụng các tham số DH nằm ở khả năng tạo ra một bảng dữ liệu rõ ràng, hệ thống hóa mối quan hệ giữa các khâu và khớp, từ đó dễ dàng xây dựng các ma trận biến đổi thuần nhất cho toàn bộ chuỗi động học của robot.
1.2. Ứng dụng trong thực tế
Trong thực tế sản xuất công nghiệp, động học thuận có nhiều ứng dụng quan trọng, bao gồm mô phỏng chuyển động của robot, kiểm tra giới hạn không gian làm việc và xác định vị trí công cụ. Các nhà thiết kế và kỹ sư sử dụng các mô hình động học thuận để dự đoán chính xác đường đi của khâu công tác cuối, giúp họ mô phỏng các tác vụ phức tạp trước khi triển khai robot vật lý.
Điều này không chỉ giúp tối ưu hóa quỹ đạo chuyển động và tránh va chạm mà còn cho phép xác định không gian làm việc tối đa mà robot có thể tiếp cận. Hơn nữa, động học thuận còn là cơ sở để tính toán vị trí chính xác của các công cụ gắp (gripper) hoặc công cụ hàn (welding tool) được gắn trên khâu công tác cuối, đảm bảo quá trình sản xuất diễn ra với độ chính xác cao nhất.
2. Động học nghịch (Inverse Kinematics)
Động học nghịch là bài toán xác định các giá trị khớp cần thiết để đưa khâu công tác cuối của robot đến một vị trí và hướng mong muốn trong không gian làm việc. Trái ngược với động học thuận, động học nghịch yêu cầu giải quyết một vấn đề phức tạp hơn, nơi chúng ta biết vị trí và hướng mục tiêu của end-effector và cần tìm các góc quay hoặc quãng trượt tương ứng của từng khớp. Bài toán này có thể có nhiều lời giải (nhiều cấu hình khớp khác nhau dẫn đến cùng một vị trí cuối), không có lời giải nào (vị trí mục tiêu nằm ngoài không gian làm việc của robot) hoặc một lời giải duy nhất.
2.1. Các phương pháp giải
Có hai nhóm phương pháp chính để giải bài toán động học nghịch: phương pháp giải tích và phương pháp số. Mỗi phương pháp có những ưu và nhược điểm riêng, phù hợp với các loại robot và yêu cầu tính toán khác nhau.

Giải tích (Analytical Solution)
Phương pháp giải tích cung cấp một lời giải đóng (closed-form solution) dựa trên các công thức toán học tường minh, thường áp dụng cho các cấu hình robot đơn giản và có ít bậc tự do. Ưu điểm nổi bật của phương pháp này là tốc độ tính toán nhanh chóng và độ chính xác cao, do không yêu cầu các phép lặp.
Tuy nhiên, nhược điểm lớn là tính khả thi hạn chế, bởi vì không phải mọi cấu hình robot đều có thể giải được bằng phương pháp giải tích. Đối với các robot có cấu trúc phức tạp, số lượng bậc tự do lớn hoặc có các khớp bất thường, việc tìm kiếm một lời giải đóng trở nên vô cùng khó khăn, thậm chí là không thể.
Số (Numerical Solution)
Phương pháp số là một cách tiếp cận linh hoạt hơn để giải bài toán động học nghịch, đặc biệt phù hợp với các cấu hình robot phức tạp, sử dụng các thuật toán lặp để tìm kiếm lời giải. Các thuật toán phổ biến bao gồm phương pháp Newton-Raphson hoặc sử dụng ma trận Jacobian pseudo-inverse. Phương pháp này bắt đầu từ một cấu hình khớp ban đầu và lặp đi lặp lại để điều chỉnh các giá trị khớp, dần dần đưa khâu công tác cuối đến vị trí mục tiêu.
Ưu điểm chính là khả năng áp dụng cho hầu hết mọi cấu hình robot, bất kể độ phức tạp. Tuy nhiên, nhược điểm là thời gian tính toán có thể lâu hơn do tính chất lặp, và thuật toán có thể mắc kẹt tại các cực tiểu cục bộ hoặc hội tụ chậm, đặc biệt khi nằm gần các điểm kỳ dị của robot.
2.2. Thách thức và cách giải quyết
Việc giải quyết bài toán động học nghịch thường phải đối mặt với một số thách thức đáng kể, bao gồm vấn đề đa lời giải, các điểm kỳ dị và giới hạn khớp của robot.
- Đa lời giải (multiple solutions): Một vị trí và hướng cụ thể của end-effector có thể tương ứng với nhiều cấu hình khớp khác nhau. Điều này đòi hỏi hệ thống điều khiển phải có khả năng lựa chọn lời giải phù hợp nhất, thường dựa trên các tiêu chí bổ sung như tránh chướng ngại vật, tối ưu hóa năng lượng hoặc duy trì chuyển động mượt mà.
- Điểm kỳ dị (singularities): Các điểm kỳ dị là những cấu hình robot mà tại đó, robot mất đi một hoặc nhiều bậc tự do, khiến ma trận Jacobian của nó bị suy biến (không khả nghịch). Tại các điểm này, robot trở nên không thể điều khiển được theo một số hướng nhất định, và việc giải động học nghịch trở nên cực kỳ khó khăn hoặc không thể. Việc nhận diện và tránh các điểm kỳ dị là rất quan trọng trong lập trình quỹ đạo robot.
- Giới hạn khớp (joint limits): Mỗi khớp của robot đều có giới hạn vật lý về góc quay hoặc quãng trượt. Hệ thống động học nghịch phải đảm bảo rằng các giá trị khớp tính toán được nằm trong các giới hạn này, nếu không robot sẽ không thể đạt được vị trí mong muốn hoặc bị hỏng hóc.
Các kỹ thuật để giải quyết những thách thức này bao gồm sử dụng thuật toán tối ưu hóa, quy hoạch quỹ đạo để tránh điểm kỳ dị, và áp dụng các phương pháp heuristic để chọn lời giải phù hợp trong trường hợp đa lời giải.

2.3. Ứng dụng trong thực tế
Trong ứng dụng thực tế của robot công nghiệp, động học nghịch là xương sống cho việc lập trình quỹ đạo robot, điều khiển thời gian thực và phối hợp chuyển động đa robot. Đối với các tác vụ như pick and place, hàn, sơn hoặc lắp ráp, động học nghịch cho phép các nhà lập trình chỉ định các điểm đích trong không gian làm việc mà không cần phải tính toán thủ công từng góc khớp.
Hệ thống điều khiển của robot tự động giải bài toán động học nghịch để tạo ra các chuyển động khớp cần thiết. Trong điều khiển thời gian thực, động học nghịch phải được giải rất nhanh để robot có thể phản ứng linh hoạt với các thay đổi môi trường hoặc lệnh điều khiển từ người vận hành. Hơn nữa, trong các hệ thống có nhiều robot làm việc cùng nhau (phối hợp chuyển động đa robot), động học nghịch là cần thiết để đồng bộ hóa chuyển động của từng robot, đảm bảo chúng không va chạm vào nhau và hoàn thành tác vụ một cách hiệu quả.
3. Các yếu tố ảnh hưởng và tối ưu hóa trong động học robot
Động học robot không chỉ là một công cụ lý thuyết mà còn là yếu tố then chốt ảnh hưởng đến hiệu suất và độ tin cậy của robot công nghiệp, đặc biệt là về độ chính xác và độ lặp lại. Độ chính xác đề cập đến khả năng của robot đạt được một vị trí mục tiêu đã định, trong khi độ lặp lại là khả năng robot quay lại cùng một vị trí nhiều lần.
Động học chính xác giúp giảm thiểu sai số vị trí, đảm bảo rằng robot thực hiện các tác vụ với sự đồng nhất cao, một yếu tố cực kỳ quan trọng trong sản xuất tự động hóa và gia công chính xác.
3.1. Độ chính xác và độ lặp lại
Động học đóng vai trò trung tâm trong việc đạt được độ chính xác và độ lặp lại cao của robot, tuy nhiên, sai số trong chế tạo và lắp ráp có thể ảnh hưởng đáng kể đến các chỉ tiêu này. Các mô hình động học lý tưởng giả định rằng các khâu robot có chiều dài chính xác và các khớp quay hoặc trượt hoàn hảo. Tuy nhiên, trong thực tế, luôn tồn tại những sai lệch nhỏ do quá trình chế tạo và lắp ráp.
Những sai số này, dù nhỏ, có thể tích lũy và dẫn đến sai lệch lớn ở khâu công tác cuối. Do đó, việc hiệu chuẩn robot (robot calibration) là một quy trình cần thiết để đo lường và bù trừ các sai số này, nâng cao hiệu suất thực tế của robot.

3.2. Tối ưu hóa thiết kế
Động học đóng vai trò quan trọng trong việc tối ưu hóa thiết kế cơ khí của robot, nhằm mở rộng không gian làm việc và tránh các điểm kỳ dị. Các nhà thiết kế sử dụng các phân tích động học để đánh giá và so sánh các cấu hình robot khác nhau, xác định chiều dài khâu và vị trí khớp tối ưu. Mục tiêu là tạo ra một robot có tầm với tối đa, khả năng cơ động cao và ít điểm kỳ dị trong không gian làm việc cần thiết cho ứng dụng cụ thể.
Việc lựa chọn số bậc tự do phù hợp cho robot cũng là một quyết định quan trọng, ảnh hưởng trực tiếp đến tính linh hoạt và khả năng thực hiện các tác vụ phức tạp của nó. Ví dụ, một robot 6 bậc tự do có thể đạt được bất kỳ vị trí và hướng nào trong không gian làm việc của nó, trong khi một robot 3 bậc tự do chỉ có thể đạt được một vị trí mà không kiểm soát được hướng.
3.3. Phần mềm và công cụ mô phỏng
Các phần mềm và công cụ mô phỏng chuyên dụng là không thể thiếu trong việc tính toán, phân tích và mô phỏng động học robot trước khi triển khai thực tế. Các công cụ này cho phép các kỹ sư thử nghiệm các chiến lược điều khiển, kiểm tra quỹ đạo và phát hiện sớm các vấn đề tiềm ẩn mà không cần đến robot vật lý, tiết kiệm đáng kể thời gian và chi phí. Một số phần mềm và công cụ phổ biến bao gồm:
- ROS (Robot Operating System): Một framework mã nguồn mở cung cấp các thư viện và công cụ để xây dựng ứng dụng robot, bao gồm cả các gói cho động học.
- MATLAB Robotics Toolbox: Một bộ công cụ mạnh mẽ trong MATLAB, cung cấp các hàm để tính toán động học, điều khiển và lập trình robot.
- CoppeliaSim (trước đây là V-REP): Một môi trường mô phỏng robot đa chức năng, cho phép mô phỏng vật lý và kiểm soát robot một cách chi tiết.
- RoboDK: Phần mềm mô phỏng và lập trình offline cho các loại robot công nghiệp khác nhau.
- Simulink: Một môi trường mô phỏng đồ họa trong MATLAB, thường được sử dụng để phát triển và kiểm tra các thuật toán điều khiển robot.
Sử dụng các công cụ này, các kỹ sư có thể nhanh chóng lặp lại các thiết kế, kiểm tra tính khả thi của các tác vụ phức tạp và tối ưu hóa hiệu suất trước khi đưa robot vào môi trường sản xuất thực tế.

4. Tương lai của động học robot trong sản xuất công nghiệp
Tương lai của động học robot trong sản xuất công nghiệp đang được định hình bởi sự tích hợp sâu rộng với các công nghệ tiên tiến như trí tuệ nhân tạo (AI), học máy, và sự phát triển của các loại robot mới. Những xu hướng này hứa hẹn nâng cao đáng kể khả năng tự chủ, thích ứng và an toàn của robot.
4.1. Tích hợp với AI và học máy
Sự tích hợp giữa động học robot với AI và học máy đang mở ra những khả năng mới cho động học thích nghi và điều khiển dự đoán. Các thuật toán học máy có thể phân tích dữ liệu cảm biến và hiệu chỉnh mô hình động học của robot trong thời gian thực, bù trừ sai số do hao mòn hoặc thay đổi tải trọng. Điều này dẫn đến động học thích nghi, cho phép robot tự động điều chỉnh chuyển động để duy trì độ chính xác trong các môi trường không xác định hoặc thay đổi.
Điều khiển dự đoán (predictive control) sử dụng các mô hình học được để dự đoán quỹ đạo chuyển động tối ưu, giúp robot thực hiện các tác vụ phức tạp một cách mượt mà và hiệu quả hơn.
4.2. Robot cộng tác (Collaborative Robots – Cobots)
Động học an toàn là một yếu tố cốt lõi cho sự phát triển của robot cộng tác (cobots), cho phép chúng tương tác an toàn với con người trong môi trường làm việc chung. Để đảm bảo an toàn, các cobots phải có khả năng phát hiện và phản ứng tức thì với sự hiện diện của con người, giảm tốc độ hoặc dừng lại để tránh va chạm.
Các thuật toán động học được phát triển đặc biệt để cho phép các cobots điều chỉnh quỹ đạo của chúng một cách linh hoạt, tạo ra các vùng an toàn động và đảm bảo rằng chúng không gây nguy hiểm cho công nhân. Điều này thúc đẩy sự hợp tác hiệu quả giữa người và máy trong các dây chuyền sản xuất.
4.3. Robot tự hành (Autonomous Robots)
Đối với robot tự hành, động học thời gian thực và khả năng lập kế hoạch di chuyển trong môi trường phức tạp là những yêu cầu thiết yếu. Các robot tự hành như AGV (Automated Guided Vehicle) và AMR (Autonomous Mobile Robot) trong kho bãi hoặc nhà máy cần phải liên tục cập nhật vị trí của chúng, xác định mục tiêu và lập kế hoạch quỹ đạo di chuyển để tránh chướng ngại vật và tối ưu hóa hiệu quả vận chuyển.
Điều này đòi hỏi các thuật toán động học phải hoạt động cực kỳ nhanh và đáng tin cậy để robot có thể thích nghi với môi trường thay đổi.

4.4. Xu hướng mới (ví dụ: robot mềm, robot sinh học)
Sự xuất hiện của các loại robot mới như robot mềm và robot sinh học đang đặt ra những thách thức động học độc đáo và yêu cầu các cách tiếp cận mới.
- Robot mềm (soft robots): Được cấu tạo từ vật liệu linh hoạt, chúng có vô số bậc tự do và biến dạng liên tục, làm cho việc mô tả và điều khiển động học trở nên cực kỳ phức tạp so với robot khớp cứng truyền thống. Các mô hình dựa trên cơ học vật liệu biến dạng và tối ưu hóa liên tục đang được phát triển.
- Robot sinh học (bio-inspired robots): Lấy cảm hứng từ các hệ thống sinh học, những robot này có thể có cấu trúc phức tạp, chuyển động uốn lượn hoặc bơi lội. Việc mô tả động học của chúng đòi hỏi các mô hình phức tạp hơn, thường kết hợp với phần tử hữu hạn hoặc các kỹ thuật mô phỏng sinh học.
5. Kết luận
Nguyên lý động học robot là nền tảng không thể thiếu cho sự hoạt động hiệu quả, chính xác và an toàn của robot công nghiệp, đóng vai trò then chốt trong quá trình chuyển đổi số của ngành sản xuất. Từ việc mô tả đơn giản chuyển động thông qua động học thuận đến việc giải quyết bài toán điều khiển phức tạp thông qua động học nghịch, động học cung cấp khung khổ toán học cần thiết để thiết kế, lập trình và vận hành robot một cách tối ưu.
Với sự tiến bộ vượt bậc của trí tuệ nhân tạo, học máy và sự ra đời của các loại robot mới như cobots và robot mềm, lĩnh vực động học robot sẽ tiếp tục phát triển, mở ra những khả năng mới cho sản xuất thông minh và tự động hóa hoàn toàn. Việc nắm vững và áp dụng hiệu quả các nguyên lý động học sẽ là chìa khóa để các doanh nghiệp và nhà nghiên cứu khai thác tối đa tiềm năng của robot, thúc đẩy năng suất, giảm chi phí và nâng cao chất lượng sản phẩm trong kỷ nguyên công nghiệp 4.0.